前回はSVMを使って線形と非線形の分類方法について学びました。今回は非線形分類の境界線の複雑さgammaの値を変更するとどのような正解率になるのかを確認してみましょう!
目次
gammaの値を大きくしてみる
まずは、gammaの値を大きくしてみましょう。今回は試しにgamma=10に変更してみます。
コード
#1 訓練データを使ってガウスカーネル法のSVMで学習モデルを作成
#2 テストデータを使って正解率を調べる
#3 テストデータを使ってこの学習モデルの分類の様子を表示する
model = svm.SVC(kernel="rbf", gamma=10) #1
model.fit(X_train, y_train)
pred = model.predict(X_test) #2
score = accuracy_score(y_test, pred)
print("正解率:", score*100, "%")
df = pd.DataFrame(X_test) #3
plot_boundary(model, df[0], df[1], y_test, "df [0]", "df [1]")参考資料:Python3年生機械学習のしくみ
実行結果
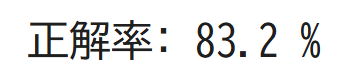
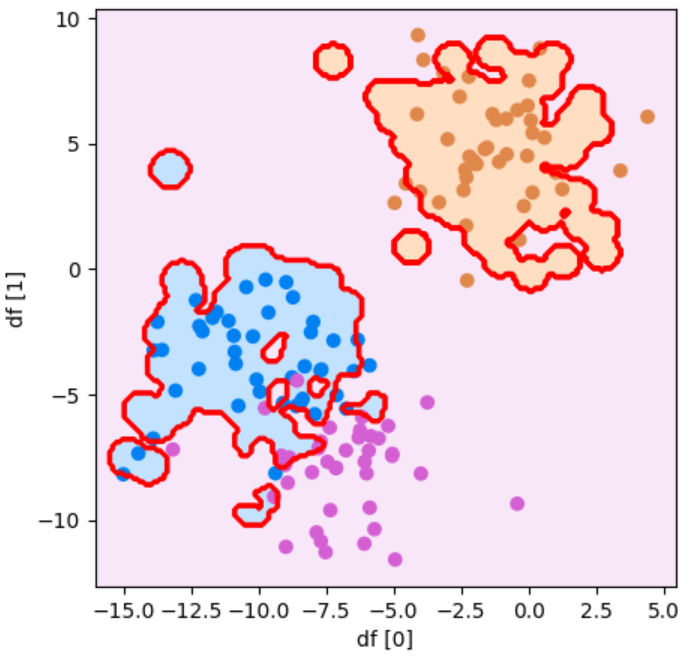
境界線がとても複雑になりましたが、ひとつひとつのデータの影響が大きくなってしまい正解率がgamma=1のときよりも低くなってしまいました…。
gammaの値を小さくしてみる
今度はgammaの値を小さくしてみましょう。今回はgamma=0.1で学習を行ってみます!
コード
#1 訓練データを使ってガウスカーネル法のSVMで学習モデルを作成
#2 テストデータを使って正解率を調べる
#3 テストデータを使ってこの学習モデルの分類の様子を表示する
model = svm.SVC(kernel="rbf", gamma=0.1) #1
model.fit(X_train, y_train)
pred = model.predict(X_test) #2
score = accuracy_score(y_test, pred)
print("正解率:", score*100, "%")
df = pd.DataFrame(X_test) #3
plot_boundary(model, df[0], df[1], y_test, "df [0]", "df [1]")参考資料:Python3年生機械学習のしくみ
実行結果
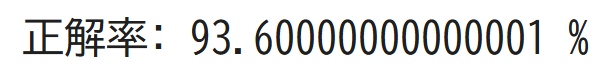
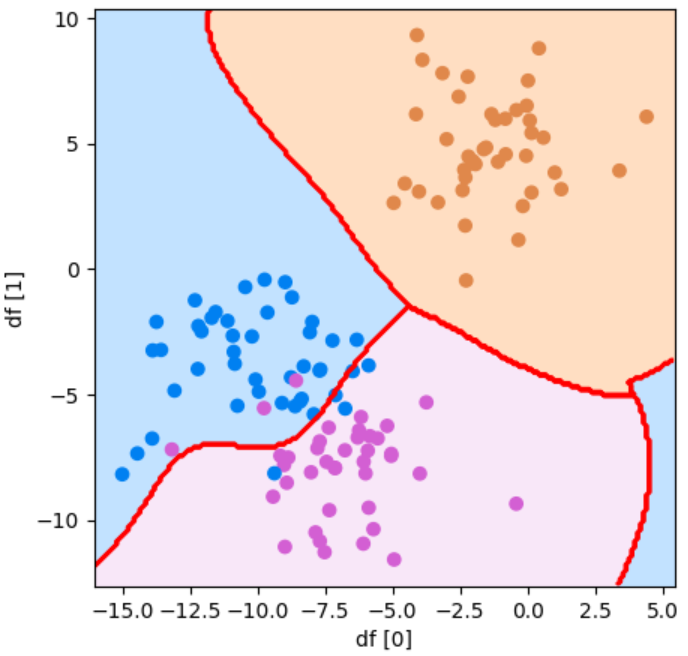
境界線が単純になりました!先ほどのgamma=10のときよりも正解率は高いですが、gamma=1のときよりは低いことがわかります。
gammaの値を自動で決めてもらう
先ほどからgammaの値を変更していますが大きくしても小さくしても正解率が思うように高くなりません。
このように、どのくらいの複雑さにすればいいかわからないときは、データの個数やばらつきから自動的に決めてくれる、「scale」や「auto」モードを使ってみましょう!
コード
#1 訓練データを使ってガウスカーネル法のSVMで学習モデルを作成
#2 テストデータを使って正解率を調べる
#3 テストデータを使ってこの学習モデルの分類の様子を表示する
model = svm.SVC(kernel="rbf", gamma="scale") #1
model.fit(X_train, y_train)
pred = model.predict(X_test) #2
score = accuracy_score(y_test, pred)
print("正解率:", score*100, "%")
df = pd.DataFrame(X_test) #3
plot_boundary(model, df[0], df[1], y_test, "df [0]", "df [1]")参考資料:Python3年生機械学習のしくみ
実行結果
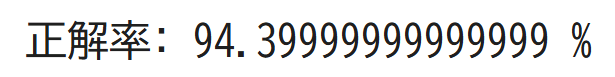
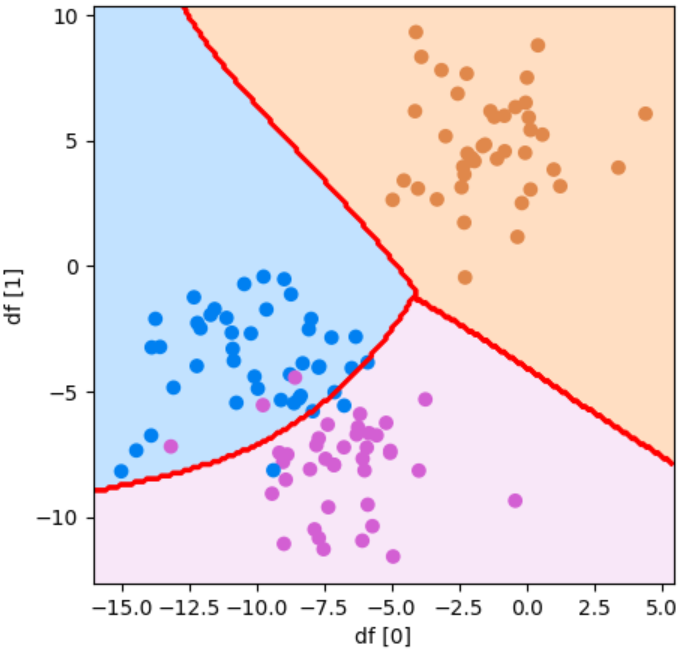
結果からわかるようにとてもきれいな分類となりました!最初の分類と正解率は変わりませんが、こちらの方がグラフで見たときに分類の状態がわかりやすいですね!
確認問題
ランダムの種:10
特徴量:2
グループ:3
ばらつき:2
点の数:500個
の塊型のデータセットをつかってSVM(サポートベクターマシン)の非線形分類を学習させて正解率を予測させましょう。
答えはコチラをクリック!
答え:
from sklearn import svm
X, y = make_blobs(
random_state=10,
n_features=2,
centers=3,
cluster_std=2,
n_samples=500)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
model = svm.SVC(kernel="rbf", gamma=0.2)
model.fit(X_train, y_train)
pred = model.predict(X_test)
score = accuracy_score(y_test, pred)
print("正解率:", score*100, "%")
df = pd.DataFrame(X_test)
plot_boundary(model, df[0], df[1], y_test, "df [0]", "df [1]")ヒント
このような散布図になるはずです!

