目次
k-NN(k近傍法)とは?
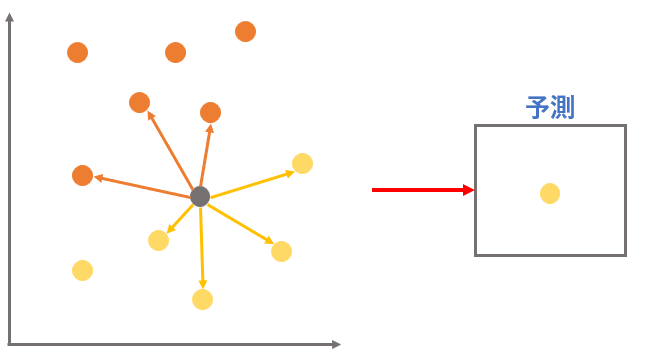
k-NN(k近傍法)とは、近くにあるデータは仲間という考え方で、調べたい値の近くにあるデータを調べて何の仲間かを予測するアルゴリズムである。
なぜ近いと仲間となるの?
散布図で見たとき、近いと特徴が似ている、遠いと特徴が似ていないといこととなるので近いデータ同士は仲間という考え方ができるのです。
k-NN(k近傍法)の使い方

上記の書式を用いて学習させたモデルにpredict命令で説明変数Xを渡すと予測結果が帰ってきます。
k-NN(k近傍法)を試してみる
決定木やランダムフォレストと同じデータである
ランダムの種:2
特徴量:2
塊数:3
ばらつき:0.5
点の数:500
のデータセットを用いてk近傍法の分類を散布図で確認してみましょう!
コード
#1 ランダムの種:2、特徴量:2、塊数:3、ばらつき:0.5、点の数:500個のデータセットを作成
#2 訓練データを使ってk近傍法の学習モデルを作成
#3 テストデータを使っって正解率を調べる
#4 テストデータを使ってこの学習モデルの分類の状態を表示
from sklearn.neighbors import KNeighborsClassifier
X, y = make_blobs(
random_state=2,
n_features=2,
centers=3,
cluster_std=0.5,
n_samples=500)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
model = KNeighborsClassifier()
model.fit(X_train, y_train)
pred = model.predict(X_test)
score = accuracy_score(y_test, pred)
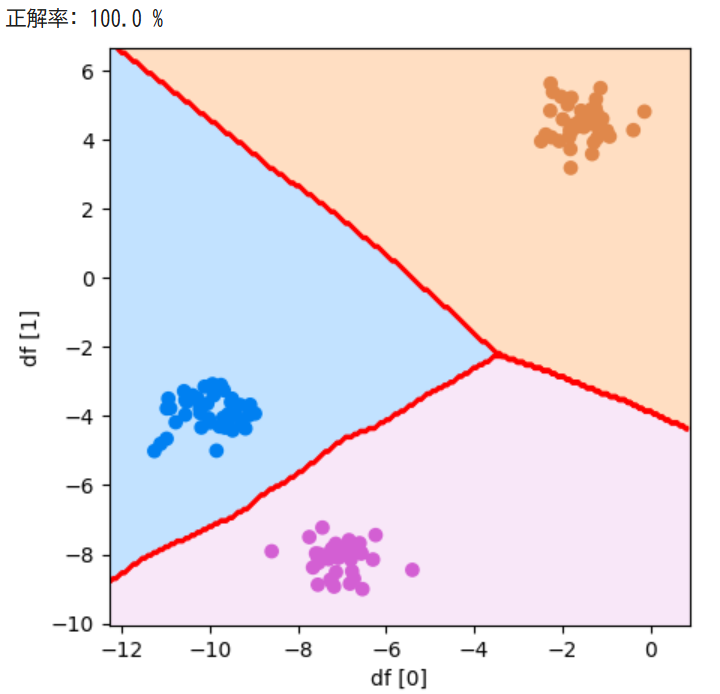
print("正解率:", score*100, "%")
df = pd.DataFrame(X_test)
plot_boundary(model, df[0], df[1], y_test, "df [0]", "df [1]")参考資料:Python3年生機械学習のしくみ
実行結果

確認問題
ランダムの種:1
特徴量:2
グループ:3
ばらつき:0.5
点の数:500個
の塊型のデータセットをつかってランダムフォレストの分類を散布図で表示してみましょう。
答えはコチラをクリック!
答え:
from sklearn.neighbors import KNeighborsClassifier
X, y = make_blobs(
random_state=1,
n_features=2,
centers=3,
cluster_std=0.5,
n_samples=500)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
model = KNeighborsClassifier()
model.fit(X_train, y_train)
pred = model.predict(X_test)
score = accuracy_score(y_test, pred)
print("正解率:", score*100, "%")
df = pd.DataFrame(X_test)
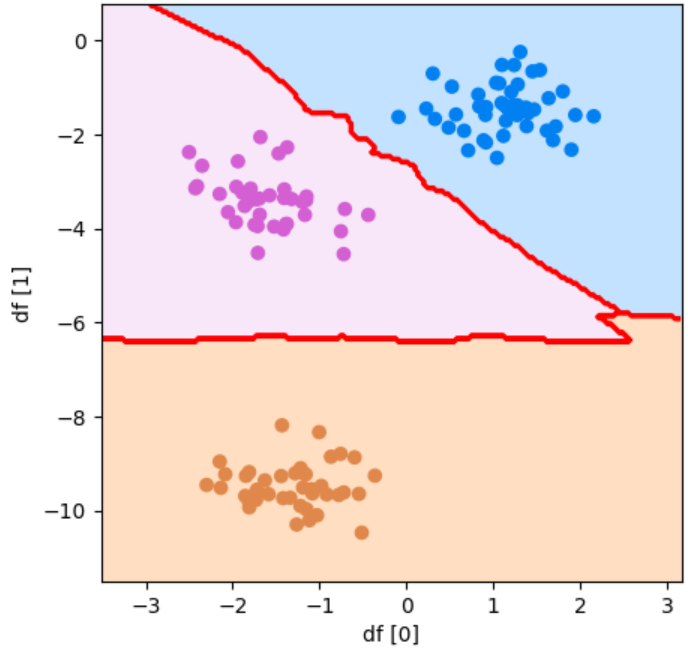
plot_boundary(model, df[0], df[1], y_test, "df [0]", "df [1]")ヒント
このような散布図になるはずです!