目次
k-means(k平均法)とは?
k-means(k平均法)とは、k近傍法と同じく近くにあるデータは仲間という考え方を扱うアルゴリズムです。k近傍法と違う点は、データ全体をグループ分けするという点です。近い者同士でグループ分けを行います。
STEP
指定したグループ数の仮の重心をランダムに決定
STEP
決定した重心から近い点を探してグループ分けを行う
STEP
各グループの平均値を求めてそれを各重心に変更&重心が動いていたらさらに続ける
STEP
2と3を繰り返す
STEP
重心が動かなくなったらグループ分けは終了
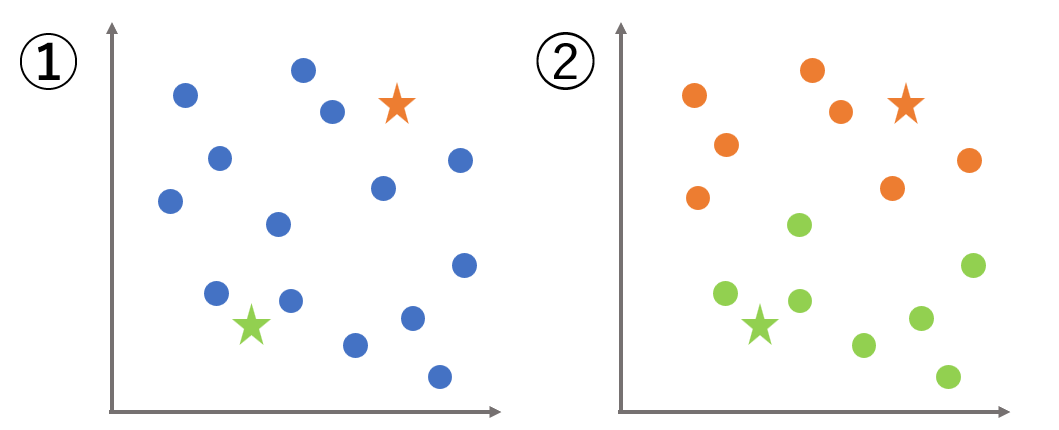
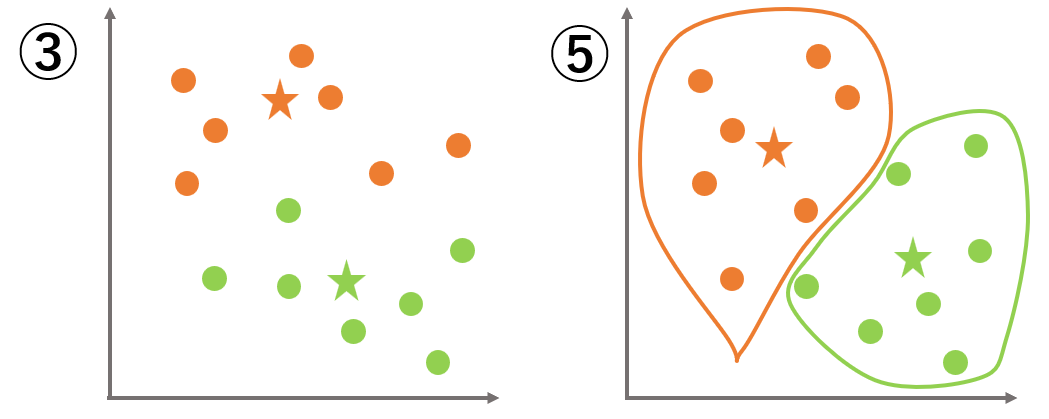
k-means(k平均法)の使い方

上記の書式を用いて学習させたモデルにpredict命令で説明変数Xを渡すと予測結果が帰ってきます。
k-means(k平均法)を試してみる
ランダムの種:2
特徴量:2
塊数:3
ばらつき:0.5
点の数:500
のデータセットを用いてk平均法の分類を散布図で確認してみましょう!
コード
#1 ランダムの種:2、特徴量:2、塊数:3、ばらつき:0.5、点の数:500個のデータセットを作成
#2 k平均法の学習モデルを作成
#3 全データでこの学習モデルの分類の状態を表示
#4 テストデータを使ってこの学習モデルの分類の状態を表示
from sklearn.cluster import KMeans
X, y = make_blobs( #1
random_state=2,
n_features=2,
centers=3,
cluster_std=0.5,
n_samples=500)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
model = KMeans(n_clusters=3) #2
model.fit(X)
df = pd.DataFrame(X) #3
plot_boundary(model, df[0], df[1], y, "df [0]", "df [1]")参考資料:Python3年生機械学習のしくみ
実行結果
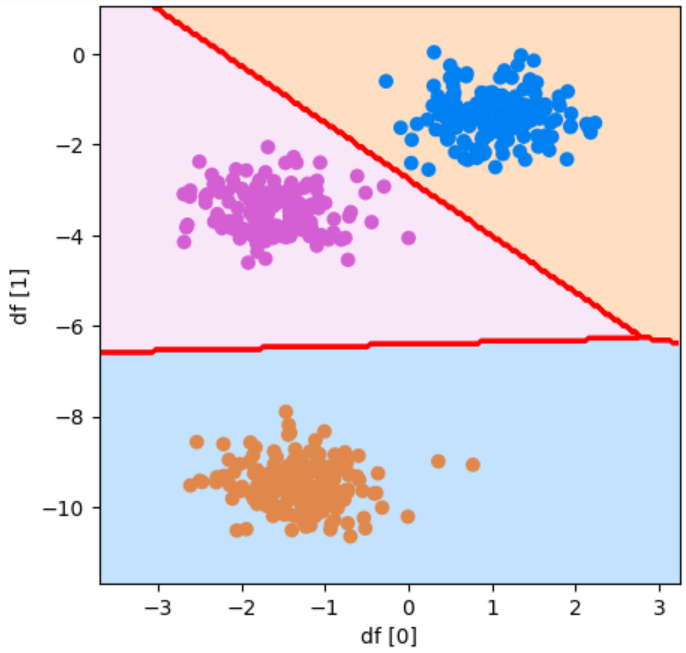
データを3つのグループに分けることができました!
2つのグループに分けてみよう!
先ほどはグループを3つに分けることができましたが、次は、2つのグループに分けるk平均法のモデルを作ってグループ分けを行ってみましょう。
コード
#1 2グループに分けるk平均法の学習モデルを作成
#2 この学習モデルの分類の様子を描画する
model = KMeans(n_clusters=2) #1
model.fit(X)
df = pd.DataFrame(X) #2
plot_boundary(model, df[0], df[1], y, "df [0]", "df [1]")参考資料:Python3年生機械学習のしくみ
実行結果
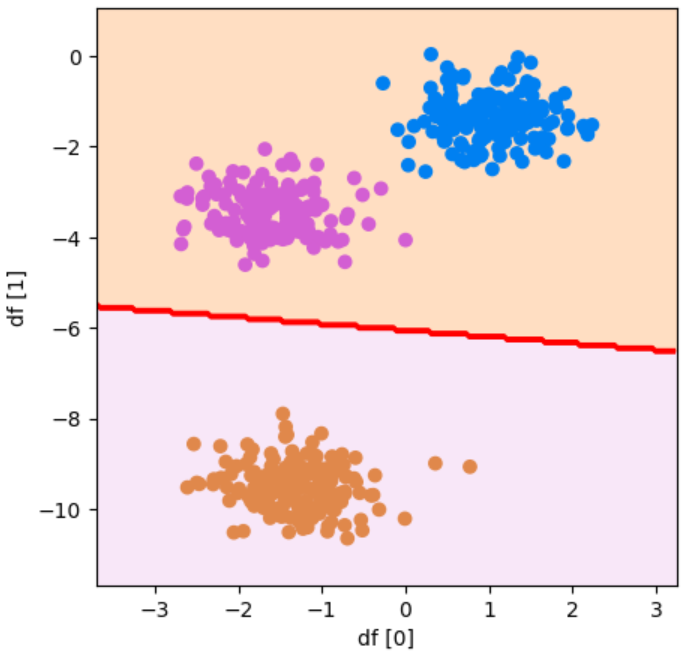
2つのグループに分けることができました!紫と青を1つのグループとして、オレンジをまた1つのグループとして認識しています。
確認問題
ランダムの種:1
特徴量:2
塊数:3
ばらつき:0.7
点の数:500
のデータセットを用いてk平均法の分類を散布図で確認してみましょう。
答えはコチラをクリック!
答え:
from sklearn.cluster import KMeans
X, y = make_blobs(
random_state=1,
n_features=2,
centers=3,
cluster_std=0.7,
n_samples=500)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
model = KMeans(n_clusters=3)
model.fit(X)
df = pd.DataFrame(X)
plot_boundary(model, df[0], df[1], y, "df [0]", "df [1]")ヒント
このような散布図になるはずです!

